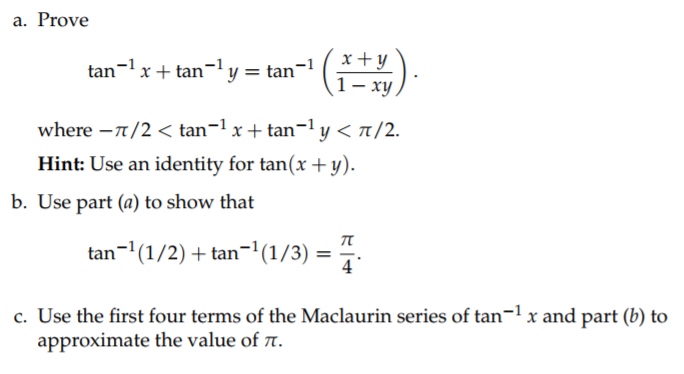
Solved A Prove Tan 1 X Tan 1 Y Tan 1 X Y 1 Chegg Com
X=1,y=1 ∴ point of intersection are (0,0) and (1,1)Tan(x y) = (tan x tan y) / (1 tan x tan y) sin(2x) = 2 sin x cos x cos(2x) = cos ^2 (x) sin ^2 (x) = 2 cos ^2 (x) 1 = 1 2 sin ^2 (x) tan(2x) = 2 tan(x) / (1
(v) x^(2)y^(2)-tan^(-1)sqrt(x^(2)+y^(2))=cot^(-1)sqrt(x^(2)+y^(2))
(v) x^(2)y^(2)-tan^(-1)sqrt(x^(2)+y^(2))=cot^(-1)sqrt(x^(2)+y^(2))-We can know at the start if it is an exact equation or not!Then the x2 y2 z z tangent plane is z = z0 0 x0 (x−x y0 x0 x y0 y , since x2y2 = z2 0) (y−y0), or z =

Answered Show That Each Function Satisfies A Bartleby
Share It On Facebook Twitter Email 1 Answer 1 vote answered by rubby (521k points) selected by Vikash KumarAnswered 5 years ago Let tan1 (1 x)/ (1 x) = y => (1 x)/ (1 x) = tan y => x = (1 tan y)/ (1 tan y) = (tan π/4 tan y)/ (1 tan π/4 tan y) => Since, tan (A B) = (tan A tan B)/ (1 tan A tan B), x = tan (π/4 y) => π/4 y = tan1x => y = π/4 tan1x 106K views Inverse Trigonometric Formulas Trigonometry is a part of geometry, where we learn about the relationships between angles and sides of a rightangled triangleIn Class 11 and 12 Maths syllabus, you will come across a list of trigonometry formulas, based on the functions and ratios such as, sin, cos and tanSimilarly, we have learned about inverse trigonometry concepts also
Y ⇡ 2 ⇡ 3⇡ 2 2⇡ 1 1 y = tan(x) x y 0 30 60 90 1 150 180 210 240 270 300 330 360 135 45 225 315 Ex 57, 17 (Method 1) If 𝑦= 〖(〖𝑡𝑎𝑛〗^(−1) 𝑥)〗^(2 ), show that 〖(𝑥^21)〗^(2 ) 𝑦2 2𝑥 〖(𝑥^21)〗^ 𝑦1 = 2 We have yGraph y=2tan(x) Find the asymptotes Tap for more steps For any , vertical asymptotes occur at , where is an integer Use the basic period for , , to find the vertical asymptotes for Set the inside of the tangent function, , for equal to to find where the vertical asymptote occurs for
(v) x^(2)y^(2)-tan^(-1)sqrt(x^(2)+y^(2))=cot^(-1)sqrt(x^(2)+y^(2))のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 | If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |  If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |
If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 | If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |  If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |
 If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 | 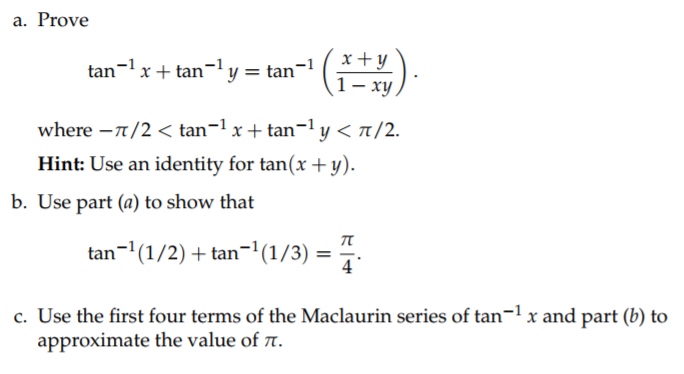 If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |  If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |
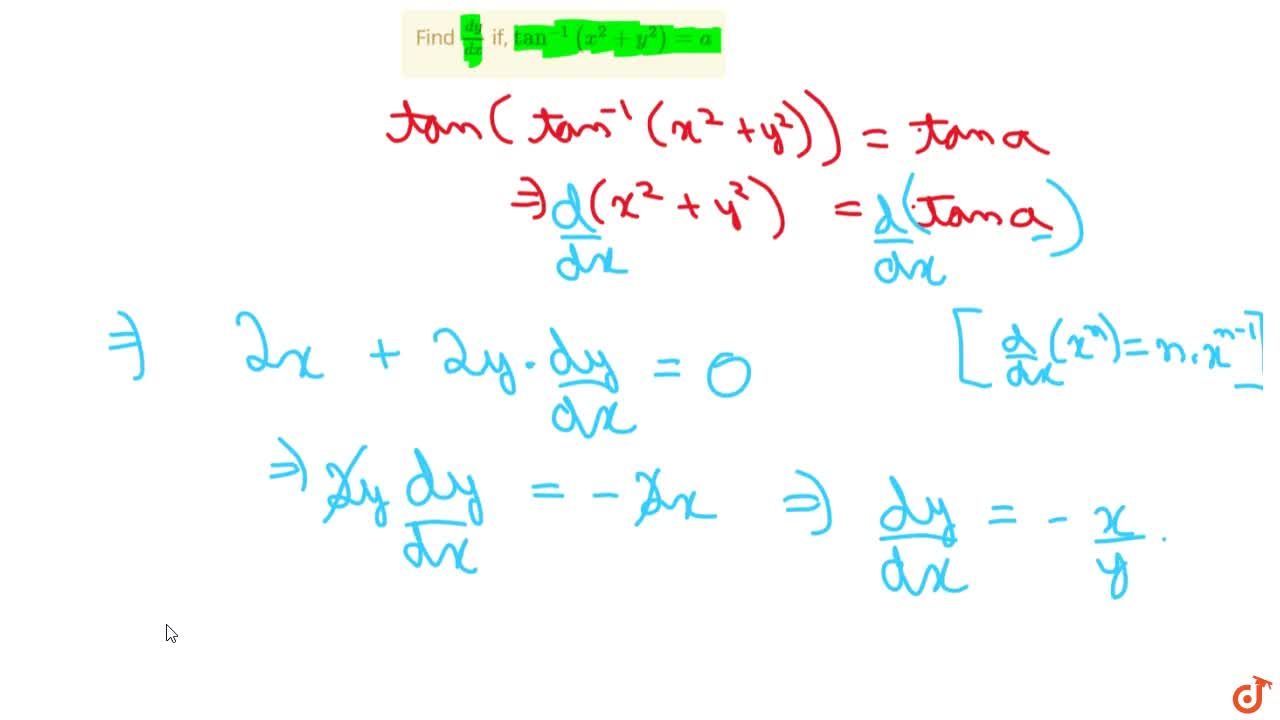 If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |  If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |  If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |
 If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |  If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |  If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |
If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |  If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |  If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |
 If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 | 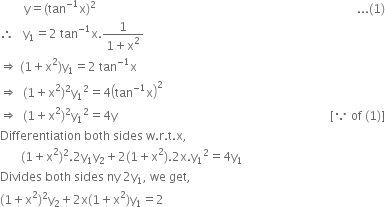 If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |  If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |
 If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |  If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |  If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |
If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 | If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 | 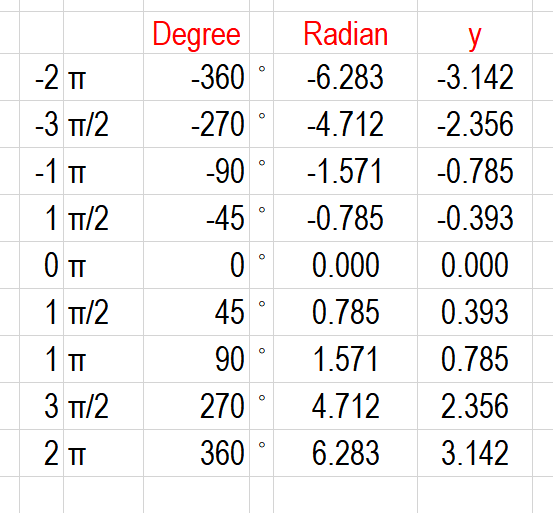 If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |
If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |  If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |  If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |
If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |  If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 | If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |
 If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |  If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 | If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |
 If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |  If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |  If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |
 If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |  If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 | If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |
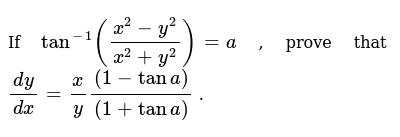 If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |  If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 | If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |
If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 | If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |  If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |
 If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 | If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |  If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |
If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |  If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |  If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |
 If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 | If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |  If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |
 If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 | 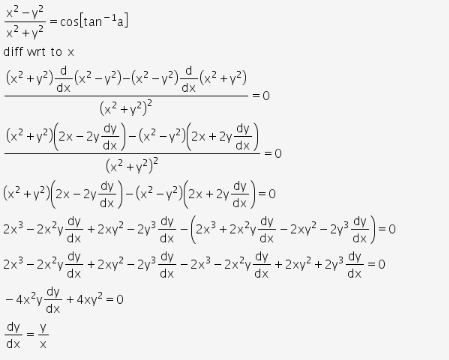 If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 | 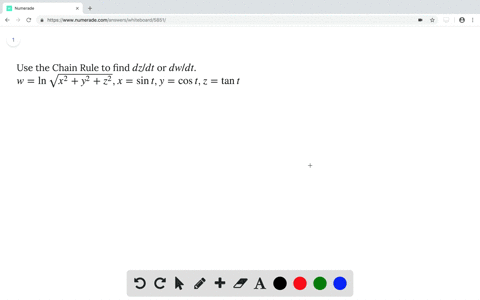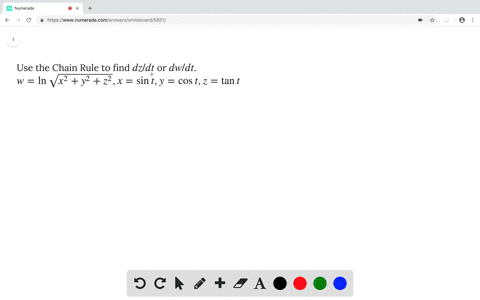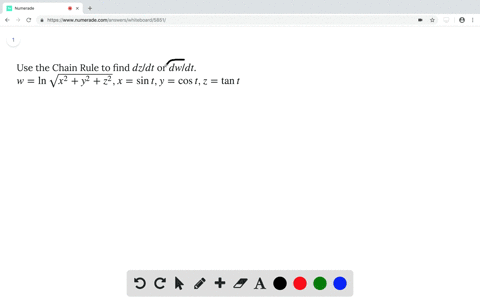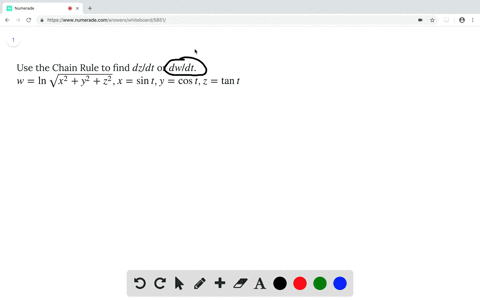 If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |
 If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |  If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 | If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |
If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 | If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |  If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |
 If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 | If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |  If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |
 If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |  If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |  If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |
 If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 | 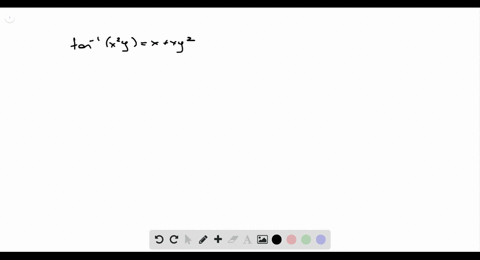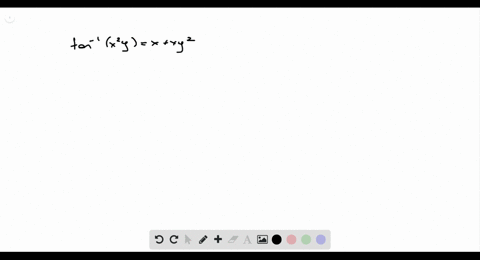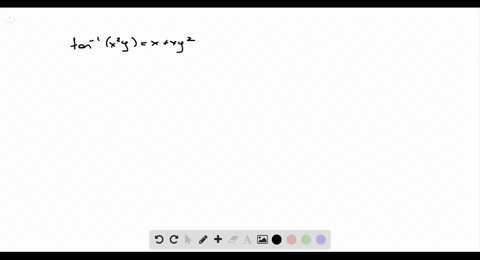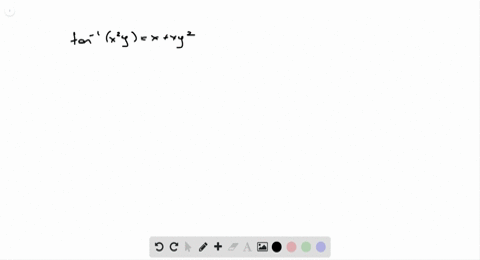 If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 | If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |
If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |  If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |  If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |
 If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 | If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |  If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |
 If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |  If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |  If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |
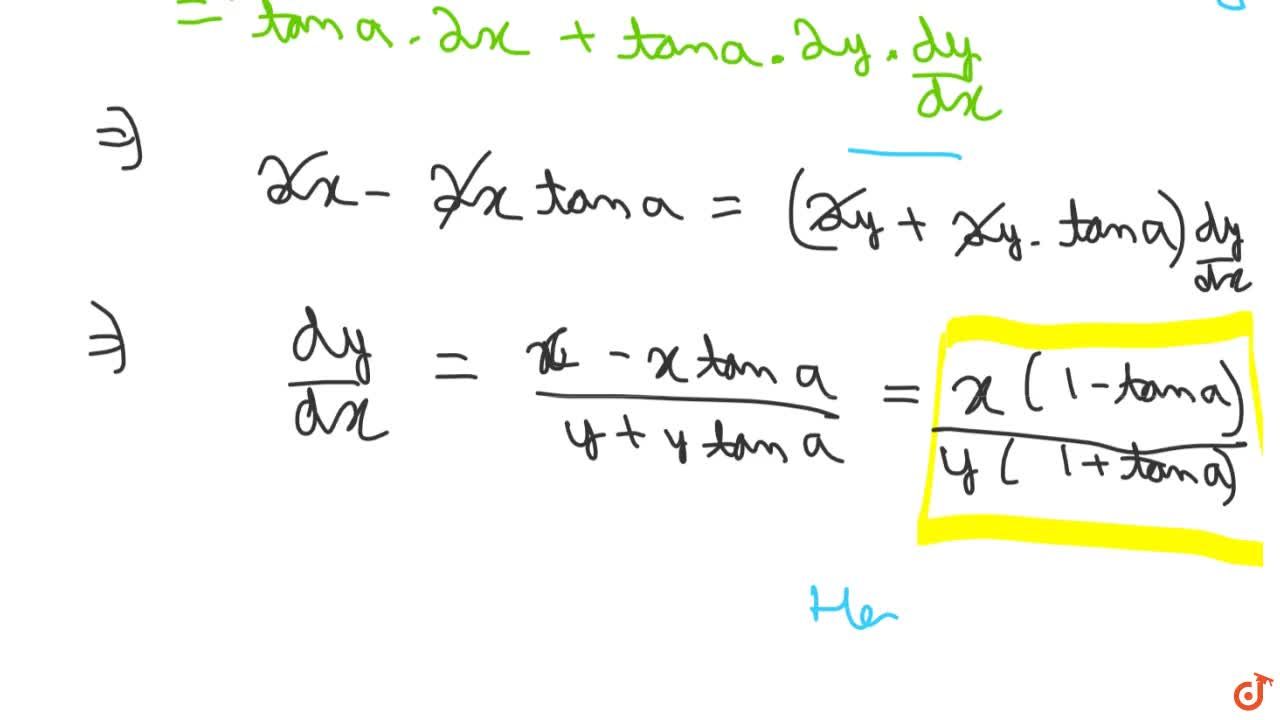 If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |  If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 | 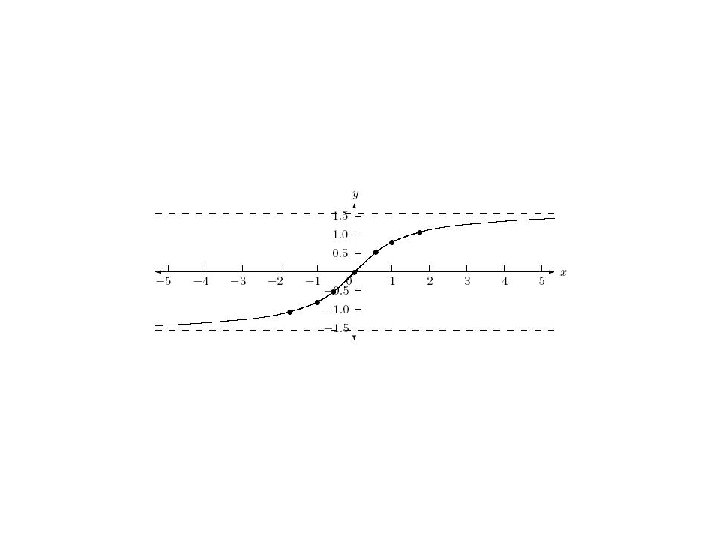 If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |
 If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 | If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 | If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |
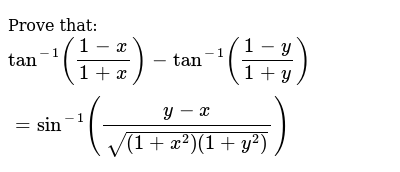 If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 | If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 | 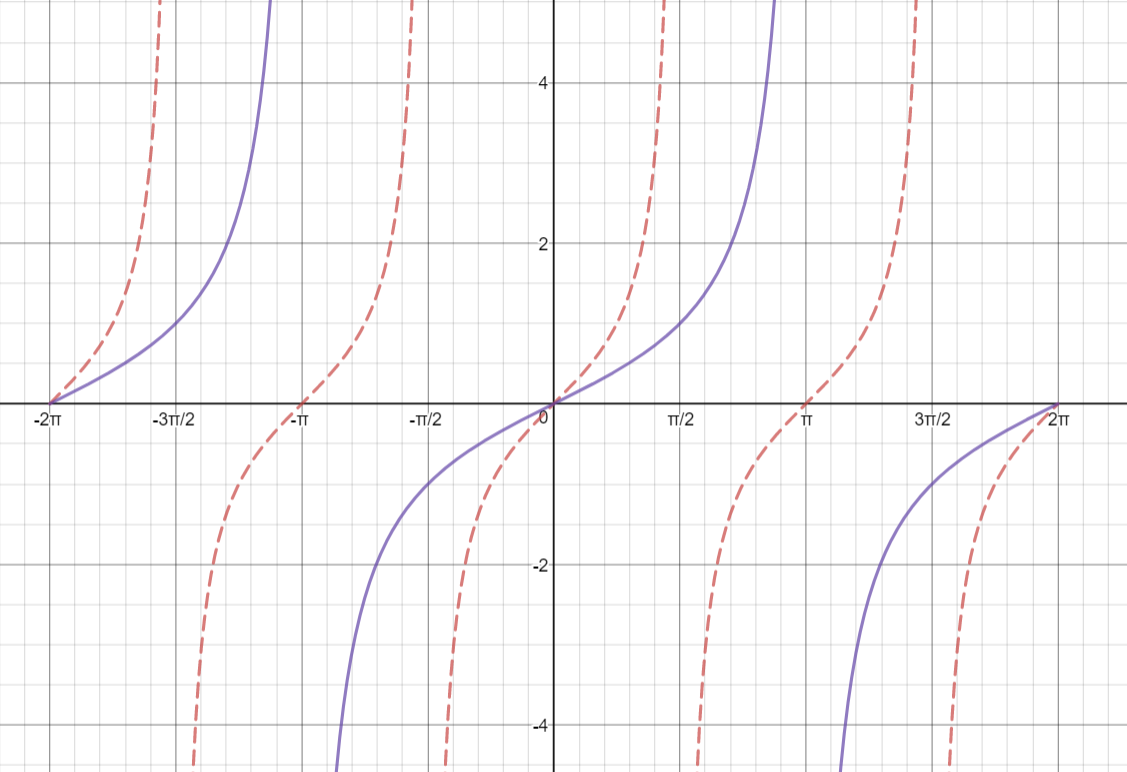 If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |
 If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |  If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |  If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |
 If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |  If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 | If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |
If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |  If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |  If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |
 If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 | If Y Tan 1x Show That 1 X 2 D 2ydx 2 2x Dydx 0 |
Therefore at (1,2,4), we get wx = −4, wy = 4, so that the tangent plane is w = 4−4(x −1)4(y −2), or w = −4x 4y x x y 2B2 a) zx = = ;1 y x x sin cos 2 y xe x 3 y e t t t sin cos 4 y e t t t sin cos (nomor 14, gunakan aturan perkalian) 5 cos sin x y x 6 2 3 1 e t y t 7 2 3 3 2 9 1 xx y x 8 yx ln( 1)2 9 yt sin (3 2)3 10 1 1 y t INTEGRAL Proses mengintegralkan suatu fungsi merupakan kebalikan turunan/derivatif Suatu fungsi f(x) dapat kita turunkan menjadi d fx() dx
Incoming Term: tan^-1(x^2-y^2/x^2+y^2)=a, if tan^-1(x^2-y^2/x^2+y^2)=a, if tan^(-1)((x^(2)-y^(2))/(x^(2)+y^(2)))=a then (dy)/(dx)=, v) if tan^(-1)((x^(2)-y^(2))/(x^(2)+y^(2)))=a then (dy)/(dx)=, cos^-1(x^2-y^2/x^2+y^2)=tan^-1a, tan x+tan y=2 and cosx cosy=(1)/(2), tan^2(x+y)+cot^2(x+y)=1-2x-x^2, x^(2)y^(2)-tan^(-1)sqrt(x^(2)+y^(2))=cot^(-1)sqrt(x^(2)+y^(2)), if tan^(-1)((x^(2)-y^(2))/(x^(2)+y^(2)))=a prove that (dy)/(dx)=(x)/(y(1+tan a)), (v) x^(2)y^(2)-tan^(-1)sqrt(x^(2)+y^(2))=cot^(-1)sqrt(x^(2)+y^(2)),




0 件のコメント:
コメントを投稿